Hacker Perspective: (some) Mathematical Ideas

Hardware for nerds

I only recall a few times when I experienced a near-religious ecstasy.

  1. When I received (then began using) my first slide rule in grade 10 (I was attending a vocational secondary school at the time)
  2. While reading the book Infinite Powers (subtitled: How Calculus Reveals the Secrets of the Universe) by Steven Strogatz
    • excerpt: the answer lies in a quip that the physicist Richard Feynman made to the novelist Herman Wouk when they were discussing the Manhattan Project. Wouk was doing research for a big novel he hoped to write about World War II, and he went to Caltech to interview physicists who had worked on the bomb, one of whom was Feynman. After the interview, as they were parting, Feynman asked Wouk if he knew calculus. No, Wouk admitted, he didn’t. “You had better learn it,” said Feynman. “It’s the language God talks.” 
  3. When I received (then began using) a Texas Instruments TI-84 Plus CE Color Graphing Calculator
    • Note: "CE" stands for "Color Enhanced graphical display" which measures 320 x 240. but it really could stand for "Computer Enhanced". Why? This gadget is really a special-purpose hand-held computer running a calculator program which can be updated with software over the USB port from your PC or Mac or Linux computer. The USB port is also used to recharge the on-board lithium battery.
No money for a graphing calculator? Don't worry because there is one built-into the CALCULATOR app that comes with Windows-11 (remember to switch the app from STANDARD to GRAPHING)
 

Learning to use your TI-84 Graphing Calculator

Texas Instruments has created a huge amount of online resources for math and science.

Unlike learning how to use a slide rule, a graphing calculator has way too many features which might trip you up for months or years. So I suggest obtaining some professional instruction from a teacher or tutor. For those unable to access either, allow me to recommend the book "TI-84 Plus CE Graphing Calculator for Dummies" by Jeff McCalla. (read how it solved my first graphing problem shown in the table 7 lines below)

The first day I was playing around with my new TI-84 I attempted to graph these two polynomials:

 equation comments
1 2x^2 no problem here with this parabola
2a -2x^2 this fails with a syntax error
equation begins with a minus sign
2b (0-2)x^2 my quick work-around
2c -2x^2 correction from the dummies guide
equation begins with the negation key
The correct answer (from the Dummies guide) instructs to use the negation key (locate the key labelled "(-)" just under the "3" key). Yikes! I've had this thing for a week but did not notice that key.

digging into e

With your graphing calculator (either a TI-84, or the Windows-11 CALCULATOR app (remember to set it to GRAPHING)), enter these six equations then punch the graph button.


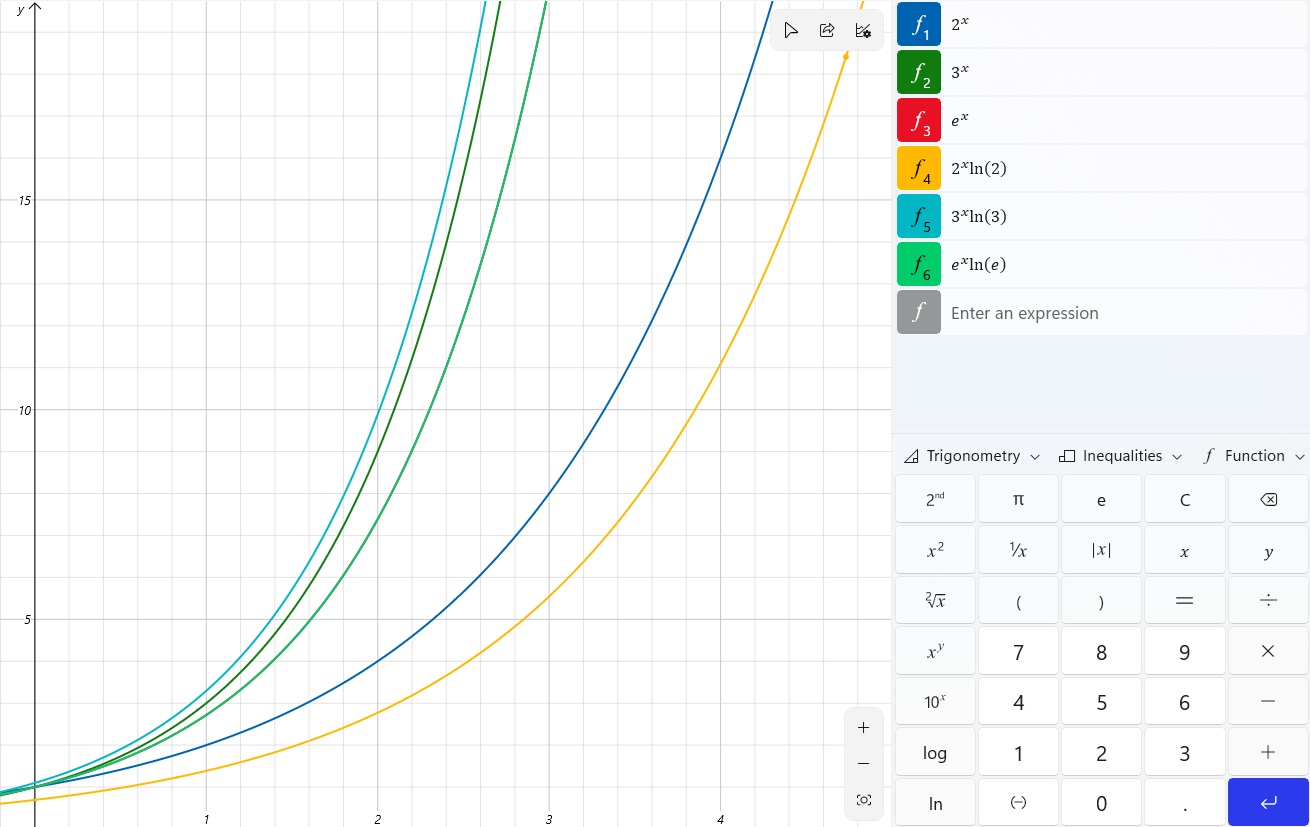
 Equation Notes
1 2^x primary
2 3^x primary
3 e^x primary
4 2^x ln(2) derivative of #1
5 3^x ln(3) derivative of #2
6 e^x ln(e) derivative of #3
Observations: comment: In 2001: A Space Odyssey we learned that the ratio of the monolith's dimensions are 1,4,9 which represent the squares of 1,2,3. Knowing what we know now about the magic of e, I wonder what the author, Arthur C Clarke, would think about raising the original series to the power of e
line X Y Z notes result
a 1 2 3 the original series
b 1 4 9 line a raised to the power of 2 Clarke's Monolith
c 1 6.58088 19.81299 line a raised to the power of e next gen monolith
Back to Home
Neil Rieck
Waterloo, Ontario, Canada.